Directed Acyclic Graphs (DAGs)

Before we can create content-addressable data structures, we have to define those structures in a way that enables us to talk about them precisely and unambiguously. For this purpose, we turn to graphs.

A graph is a mathematical abstraction that is used to represent relationships among a collection of objects. It is common to use the term node to refer to an object in a graph, and the term edge to refer to a relation among objects. Most commonly, graphs are used to represent pairwise relationships between objects. For example, a graph might be used to map the roads connecting pairs of cities, or the friendships between students in a school.

The example file hierarchy we introduced in the previous lesson also forms a graph (the directories and files act as our nodes, and the relationship between a directory and the files it contains gives us our edges). We’ve depicted it again in the figure below:

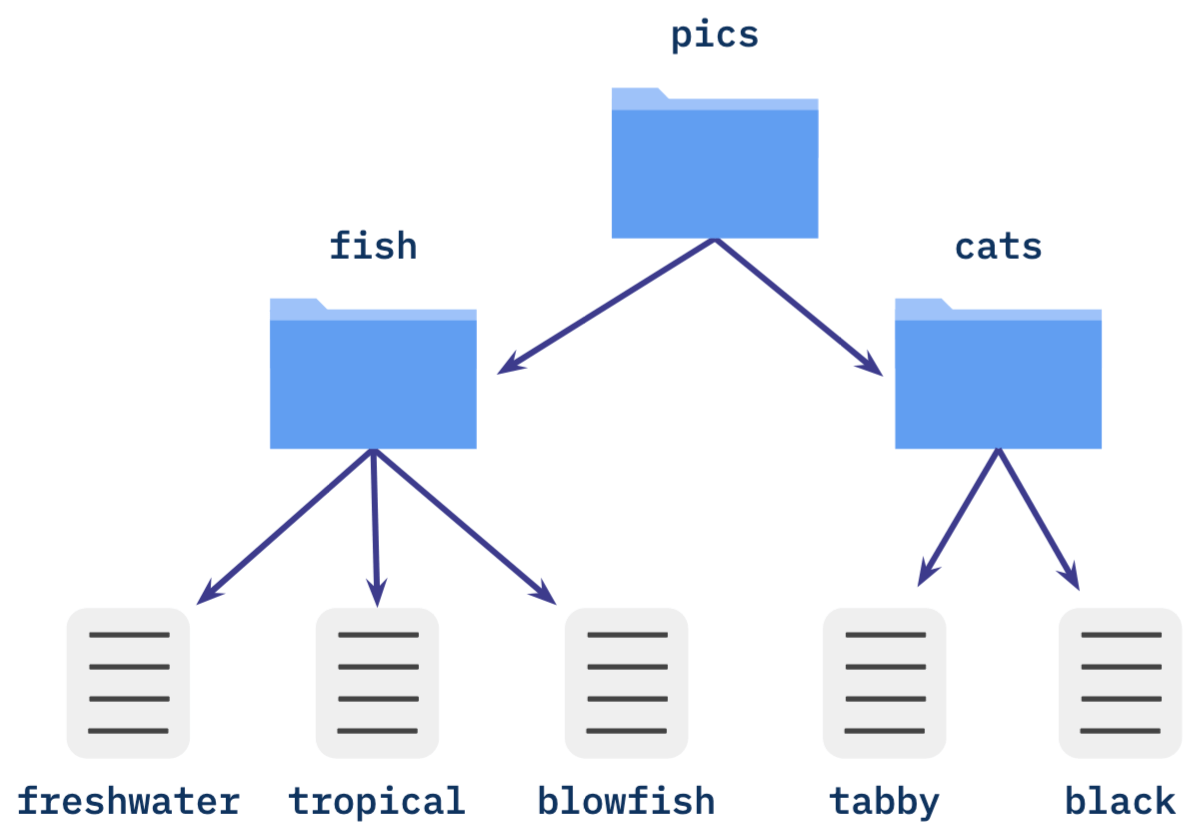
Given a graph, we can imagine starting at a node and moving along its edges to get to another node. For example, we might start at the root directory, "pics", in the figure above, and progressively move deeper into the hierarchy to reach a desired file.

Directed Graphs

A graph is called directed if each edge has some sense of direction. In the figure above, for example, edges represent containment: a directory contains a file, but a file does not contain its directory. The relationships between nodes only properly associate in one direction, and this direction is indicated by a single-headed arrow. Genealogical terms like ancestor, descendent, parent and child are frequently used to refer to the nodes in a directed graph. For example, in our figure, the node corresponding to the "cats" directory would be said to be parent to the two file nodes it contains.

Nodes that have no parents are frequently called root nodes, while those without children are called leaf nodes. Nodes with both parents and children are called intermediate nodes, as they lie between the graph’s roots and leaves. It’s also common to use the term non-leaf to refer to both intermediate nodes and root nodes.

Acyclic Graphs

A graph is called acyclic if there are no loops in the graph - i.e., given any node in the graph, there is no way to navigate from that node back to itself along the graph’s edges. In a directed graph like our file hierarchy, we can only move from parent nodes to child nodes.

Directed Acyclic Graphs

A graph that is both directed and acyclic is called, appropriately enough, a directed acyclic graph. It turns out, these are a very commonly studied structure—so common, in fact, that the acronym DAG is frequently used to refer to them! Hierarchical data in particular is very naturally represented via DAGs.